What is Tree Traversal?

In a tree data structure, traversal refers to accessing nodes in a particular order. In a binary tree, each node can have a maximum of two other nodes.

A well-known data structure is a binary tree. Additionally, there is a Binary Search tree (BST). There are several uses for this style of traversal. The level order traversal is employed to determine the depth between any two nodes. Another type of tree known as “AVL” requires measuring the height of each node. Although a binary tree may be represented as an array, we’ll use a structure and pointer to refer to the next node in order to save memory.

Traversing a tree have a particular order as follows:

• For Inorder, you traverse from the left subtree to the root then to the right subtree.
• For Preorder, you traverse from the root to the left subtree then to the right subtree.
• For Post order, you traverse from the left subtree to the right subtree then to the root.

Root: The topmost node in the tree.

Parent: A node with a child or children.

Child: A node extended from another node (parent node).

Leaf: A node without a child.

Types of Tree Traversal

• Pre-order traversal
• Post-order traversal
• In-order traversal

InOrder Traversal

1. Left, Root, Right
2. Root node will be in Middle Position
3. Traverse the left subtree, i.e., call Inorder(left->subtree)
4. Visit the root.
5. Traverse the right subtree, i.e., call Inorder(right->subtree)

Example

Given Nodes => D B E A F C G

Step 1: Identify the root node. In InOrder, middle element always root node. so here A is root Node

D B E A F C G

Step 2: DBE -> Left Sub Tree, FCG -> Right Sub Tree

Step 3: Traverse from the left subtree to the root (DBE) -> (Left, Root, Right)

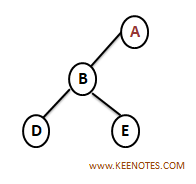
Step 4: Traverse from the right subtree to the root (FCG) -> (Left, Root, Right).

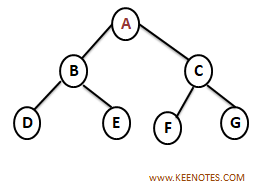
PreOrder Traversal

1. Root, Left, Right
2. Root node will be in First Position
3. Visit the root.
4. Traverse the left subtree, i.e., call Preorder(left->subtree)
5. Traverse the right subtree, i.e., call Preorder(right->subtree)

Example

Given Nodes => A B D E C F G

Step 1: Identify the root node. In PreOrder, first element always root node. so here A is root Node

A B D E C F G

Step 2: BDE-> Left Sub Tree, CFG-> Right Sub Tree

Step 3: Traverse from the left subtree to the root (BDE) -> (Root, Left, Right)

Step 4: Traverse from the right subtree to the root (CFG) -> (Root, Left, Right).

PostOrder Traversal

1. Left, Right, Root
2. Root node will be in Last Position
3. Traverse the left subtree, i.e., call Postorder(left->subtree)
4. Traverse the right subtree, i.e., call Postorder(right->subtree)
5. Visit the root

Example

Given Nodes => D E B F G C A

Step 1: Identify the root node. In PostOrder, LAST element always root node. so here A is root Node

D E B F G C A

Step 2: DEB-> Left Sub Tree, FGC-> Right Sub Tree

Step 3: Traverse from the left subtree to the root (DEB) -> (Left, Right, Root)

Step 3: Traverse from the right subtree to the root (FGC) -> (Left, Right, Root)