
RSA stands for Rivest, Shamir, Adleman. It is a public key encryption technique used for secure data transmission especially over the internet.
It makes use of prime numbers and the factoring problem.
It is a reliable yet slow algorithm for data encryption/ decryption.
It is an Asymmetric Cryptographic Algorithm
Two Keys
- Public Key
- Private Key
Public key: It comprises two numbers, in which one number is the result of the product of two large prime numbers. This key is provided to all the users.
Private key: It is derived from the two prime numbers involved in public key and it always remains private.
If public key of users is used for encryption then we have to use the private key of same user for decryption. The RSA Scheme is a block cipher in which the plain text and cipher text are integers between 0 and (n-1) for the same value n.
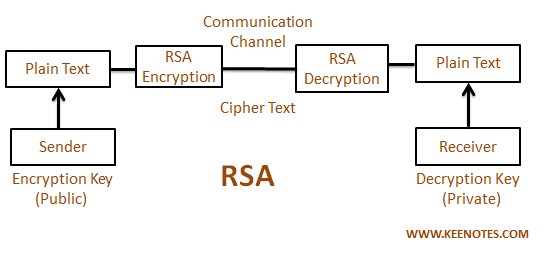
The RSA algorithm involves four steps for data transmission which are as follows:
- Key Generation
- Key distribution
- Encryption
- Decryption
Key Generation
- Select 2 large prime numbers p & q
- Calculate n=p*q
- Calculate φ(n) = (p-1)(q-1)
- Choose value of e => 1 < e < φ(n) and GCD(e, φ(n))=1
- Calculate d = e pow 1 mod φ(n) => ie. ed = 1 * mod φ(n)
- Public Key = {e, n}
- Private Key = {d, n}
Formula for Finding the Encryption Text
To find cipher text C = (Message)^e mod n
C = M^e mod n
Formula for Finding the Decryption Text
To find the Message M = (Cipher Text)^d mod n
M = C^d mod n
Example 1:
RSA Algorithm is used by choosing 2 prime numbers p=3, q=11 and public key e=7. calculate the value of d. Also find the encryption and decryption key.
Let p=3, q=11, e=7
n=p*q = 3*11 = 33
φ(n)=(p-1)(q-1) = (3-1)(11-1)
= (2)(10)
= 20
so, let e=7, as 1<7<20 and gcd(20,7)=1
Now, ed = 1*mod φ(n)
ed mod φ(n) = 1
7*d mod 20 = 1
if d=3, then 21 mod 20 = 1
e=7, d=3, n=33
Public key = {e, n} = {7,33}
Private Key = {d, n} = {3,33}
FOR ENCRYPTION TEXT
To find cipher text(Encryption Text) C = pow(M,e) mod n
C = M^e mod n Where M is message(raw text/plain text)
Let M=31, e=7 then Encryption Text C = pow(31,7) mod 33
= 31^7 mod 33
(7 times multiplication of 31 => 31*31*31*31*31*31*31)
= 27512614111 mod 33
= 4
FOR DECRYPTION TEXT
To find the Message M = pow(C, d) mod n
M = C^d mod n Where C is Cipher Text(Encrypted)
Let C=4, d=3, then Decryption Text M = pow(4, 3) mod 33
= 4^3 mod 33
= 64 mod 33
Decryption Text M = 31
Advantages of RSA
- Easy to implement RSA algorithm.
- Safe and secure for transmitting the sensitive data
- Sharing public key to users is easy.
- Cracking RSA algorithm is very difficult as it involves complex mathematics.
Disadvantages of RSA
#Asymmetric Cryptographic Algorithm #Decryption #Encryption #RSA #RSA Algorithm
- Sometimes a third party is needed to confirm the validity of public keys.
- For public data encryption, such as electoral voting, RSA cannot be utilized.
- Decryption requires a large amount of processing power on the receiver’s end.
- It may fail sometimes because for complete encryption both symmetric and asymmetric encryption is required and RSA uses asymmetric encryption only.
- It has slow data transfer rate due to large numbers involved.